| Laboratório de Análise Numérica

 

Analytical and numerical methods in shape and topology optimization.

Shape optimization and topology optimization are techniques based on rigorous mathematical results, well established and widely used in several areas of Engineering. The numerical simulations performed in LAN are closely followed and validated by theoretical studies. Here are some related papers.


 

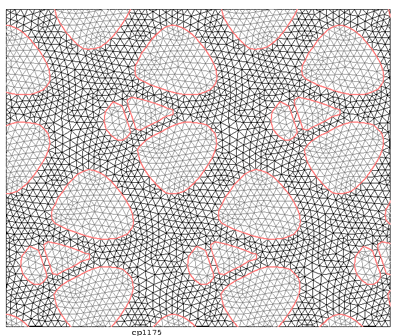
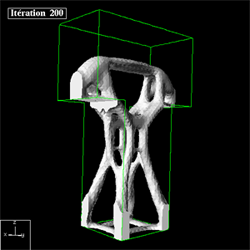
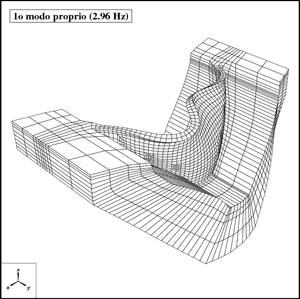
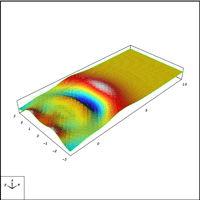
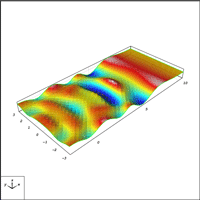
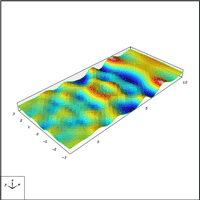
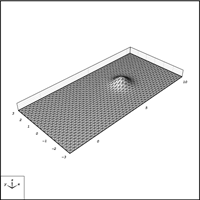
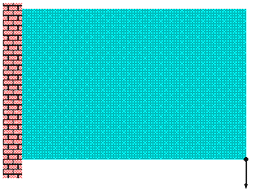Cristian Barbarosie and Anca-Maria Toader have developed work on periodic microstructures, which appear naturally through relaxation of certain structural optimization problems. This study is based on theoretical tools like homogenization theory which describes stationary phenomena like linear elasticity, and Bloch wave theory which describes dynamic phenomena like vibration and wave propagation. In this framework, the optimization techniques for (macroscopic) solid bodies are transposed to the microscopic level by means of variations in the geometry and in the topology of porosities and inclusions in the periodicity cell. Here are some published papers : C. Barbarosie, A.-M. Toader, Shape and Topology Optimization for Periodic Problems Part I: The shape and the topological derivative, Structural and Multidisciplinary Optimization, Volume 40, Numbers 1-6 / January, 2010, 381-391, preprint CMAF Pre-2008-016; Part II: optimization algorithm and numerical examples, Structural and Multidisciplinary Optimization, Volume 40, Numbers 1-6 / January, 2010, 393-408, preprint CMAF Pre-2008-017. See on the right the animation of the optimization process of a periodic microstructure whose bulk modulus is being maximized.

 

 

The work on Bloch waves began in 2004 (see the paper C. Barbarosie, M.M. Neves, Periodic structures for frequency filtering: analysis and optimization, Computers & Structures, Volume 82, Issue: 17-19, Pages: 1399-1403, Published: 2004) and continues to the present day (see the abstract of the communication presented at ECCM 2010 Paris)

Locally periodic microstructures were considered as well, in the sense that the microgeometry is allowed to vary from element to element in the macroscopic body. See the preprint CMAF Pre-2009-021 and the three examples of optimized (locally periodic) microstructures.

In all examples, the body occupies a 2x1 rectangle and is clamped on its left side.

 

First example : one force in the middle of the right side (see the figure above left). In the figure above right, the optimized structure is represented. Click on the image to see details.

Second example : one force in the lower right corner (see the figure above left). In the figure above right, the optimized structure is represented. Click on the image to see details.

Third example : three forces on the right side acting independently of each other (see the figure above left). In the figure above right, the optimized structure is represented. Click on the image to see details.

 

Anca-Maria Toader has developed work on shape and topology optimization using level set methods jointly with G. Allaire, F. Jouve and F. de Gournay -- an example is available here.

 

In particular, examples involving "following forces" (like pressure) were treated; a generalization of this case will be developed for large scale problems with the goal of optimizing dam design.

The application of optimization techniques to dam design is not at all straightforward since it involves unusual objective functionals and constraints which require specific mathematical techniques to be developed. An important goal from the engineering point of view, is the material coefficient identification in existing structures. Parametric optimization and free material design are two techniques recently used by Anca-Maria Toader, Paulo Vieira and Sérgio Oliveira in inverse problems to identify the degree of damage in dams, see the slides of the communication presented at ECCM 2010 Paris.

Numerically computed eigenvalues and eigenmodes of the Cabril dam by Paulo Vieira are available here. Below are the first two eigenmodes.

 

 

Cristian Barbarosie works on modelling of abstract surfaces, with applications in Finite Elements.

The image on the right represents a triangulation of a Klein surface (mesh built directly using a Python program, drawn with xd3d.

 

Analytical and numerical models for Surface Water Waves.

Boussinesq-type equations are widely used for modeling the propagation and generation of surface water waves. Due to the high order of the equations involved in the models, the finite element method is not easy to implement for this type of problems.

Nuno Lopes and his Phd. Supervisors, L.Trabucho (CMAF and DM-FCT-UNL) and P. Pereira (ISEL and CEFITEC), are developing an enhanced Boussinesq-type system along with a Continuous/Discontinuous Galerkin Finite Element method for the numerical solution of the referred fourth-order PDE system.

See the slides of the communication presented at ECCOMAS CFD 2010 Lisbon.

Example: Propagation of waves generated by an underwater slide moving in an horizontal bottom with a subcritical constant speed.

Initial slide position time=0s
Surface elevation at time=1s
Surface elevation at time=6s
Final slide position time=6s
   
Water Surface Animation

 

| Arquivo | Public List LAN